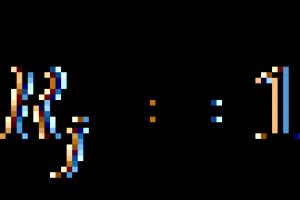Достаточные признаки экстремума. Необходимые и достаточные условия существования экстремума функции в точке

Необходимый признак экстремума можно сформулировать и так: если точка M (x 0 , y 0 ) является точкой локального экстремума дифференцируемой функции z = f (x , y ), то вектор градиента этой функции в этой точке будет нулевым вектором, т.е. .

Точки, в которых частные производные первого порядка функции двух переменных равны нулю, называются стационарными точками.

Для формулировки достаточного признака экстремума функции двух переменных нам понадобится матрица дифференциала второго порядка этой функции, записанного в виде квадратичной формы:

А также определитель этой матрицы, который можно записать в следующем виде:

Достаточный признак экстремума

Замечание. Если в стационарной точке М : Δ = АВ – С 2 = 0, то наличие экстремума возможно, но для этого требуется проведение дополнительных исследований.

ПРИМЕР: Найти экстремумы функции

Вычислим частные производные первого и второго порядка данной функции:

Для нахождения стационарных точек приравняем к нулю частные производные первого порядка и получим систему уравнений:

или:

Решая эту систему, получим две стационарные точки М (0, 0) и N (1, 1/2).

Для выяснения наличия экстремумов и их характеров в этих точках вычислим значения частных производных второго порядка последовательно в каждой точке.

Для стационарной точки М (0, 0) получим:

Поскольку: Δ = АВ – С 2 = - 36 < 0, в этой стационарной точке экстремума нет.

Для стационарной точки N (1, 1/2) получим:

Поскольку Δ = АВ – С 2 = 108 > 0 и A = 6 > 0, заключаем, что в этой стационарной точке будет локальный минимум данной функции. Причем значение функции в точке минимума будет равно 0.

Метод наименьших квадратов

В практических приложениях, в том числе и экономических, часто возникает задача сглаживания некоторых экспериментально полученных зависимостей. То есть задача по возможности точно отразить общую тенденцию зависимости y от x , исключив случайные отклонения от этой общей тенденции, обусловленные неизбежными погрешностями экспериментальных или статистических данных. Такую сглаженную зависимость обычно ищут в виде формулы. При этом формулы, служащие для аналитического представления зависимостей опытных или экспериментальных данных, принято называть эмпирическими.

Задача поиска подходящей эмпирической формулы обычно разбивается на два основных этапа. На первом этапе устанавливают, или выбирают, общий вид такой зависимости y = f (x ), т.е. решают, является ли данная зависимость линейной, квадратичной, показательной, логарифмической и т.д. При таком выборе часто привлекаются дополнительные соображения, как правило, нематематического характера. На втором этапе находят неизвестные параметры выбранной эмпирической функции, используя только массив экспериментально полученных данных.

Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов в качестве неизвестных параметров эмпирической функции f (x ) выбирают такие значения, чтобы сумма квадратов “невязок” δ i (отклонений “теоретических” значений функции от экспериментально полученных значений) была бы минимальной, т.е.:

где и - экспериментальные данные, а n – общее количество пар этих данных.

Рассмотрим простейшую задачу такого рода. Пусть в качестве эмпирической функции выбрана линейная функция, т.е. (рис. 22), и необходимо найти такие значения параметров a и b , которые доставят минимум функции: .

Очевидно, функция будет функцией двух переменных a и b до тех пор, пока не найдены и не зафиксированы их “наилучшие” значения, поскольку все и есть постоянные числа, найденные экспериментально. Поэтому для нахождения параметров прямой, наилучшим образом согласованной с опытными данными, достаточно решить систему уравнений:

После соответствующих вычислений производных и тождественных преобразований эта система может быть представлена в виде системы нормальных уравнений :

Эта система линейных уравнений имеет единственное решение, которое может быть найдено по правилу Крамера:

;

Таким образом, наилучшим линейным приближением экспериментальной зависимости по методу наименьших квадратов будет являться прямая .

ПРИМЕР: Зависимость между прибылью предприятия Y и стоимостью основных фондов Х , выраженных в условных единицах, задается таблицей.

Х
Y

Для выяснения вида эмпирической формулы связи построим график экспериментальной зависимости (кружки на рис. 23). По расположению экспериментальных точек на графике можно предположить, что зависимость между Х и Y является линейной, т.е. имеет вид:

Для определения числовых значений параметров а и b проведем расчет коэффициентов системы нормальных уравнений, а для удобства сведем вычисления в таблицу.

По данным таблицы:

Подставляя найденные значения (с учетом того, что n = 7) в формулы для расчета параметров а и b , найдем:

Таким образом, эмпирическая зависимость имеет вид (на рис. 23 изображена сплошной прямой): y = 0,557x – 5,143.

ВОПРОСЫ для самоконтроля знаний по теме 6:

1. Задает ли уравнение функцию нескольких переменных?

Билет №1

первообразной функцией Теорема Доказательство неопределённым интегралом

Точка (X 0 ;Y 0) называется точкой максимума точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0).

Докозательство:

Билет №2

Доказательство Геометрический смысл

частным приращением частной производной Геометрический смысл

Билет №3

19. Определение точки максимума и минимума функции z=f(x,y). Точка (X 0 ;Y 0) называется точкой максимума функции z=f(x;y), если существует такая δ-окрестность точки (X 0 ;Y 0), что выполняется неравенство f(x;y)точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ><0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №4 Определённым интегралом Свойства Доказательство. в точке с координатами (x;y;z) .Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.Предположим, что функция u(x;y;z) непрерывна и имеет непрерывные производные по своим аргументам в области D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, где E 1 , E 2 , E 3 стремятся к нулю при Δl→0. Разделим всё равенство на Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Равенство можно представить так: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Перейдя к пределу, получим Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Билет №5

1. Первообразная функция. Теорема о разности двух первообразных (с доказательством). Неопределенный интеграл: определение Функция F(x) называется первообразной функцией f(x) на интервале (a;b), если для любого x∈(a;b) выполняется равенство F"(x)=f(x).Теорема . Если функция F(х) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задаётся формулой F(x)+C, где С=const.Доказательство . Функция F(x)+C является первообразной f(x). Действительно, (F(x)+C)"=F"(x)=f(x). Пусть Ф(х) - некоторая другая, отличная от F(x), первообразная функция f(x), т.е. Ф"(х)=f(x). Тогда для любого x∈(a;b) имеем (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x)-f(x)=0. А это означает, что Ф(х)-F(x)=C, C=const. Следовательно, Ф(x)=F(x)+C.Множество всех первообразных функций F(x)+C для f(x) называется неопределённым интегралом от функции f(x) и обозначается символом ∫f(x)dx.

19. Определение точки максимума и минимума функции z=f(x,y). Точка (X 0 ;Y 0) называется точкой максимума функции z=f(x;y), если существует такая δ-окрестность точки (X 0 ;Y 0), что выполняется неравенство f(x;y)точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0). 20. Достаточный признак существования экстремума функции z=f(x;y). (формулировка). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ>0, то функция f(x;y) в точке (X 0 ;Y 0) имеет экстремум: максимум, если A<0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №6

3. Вычисление определенного интеграла по отрезку. Формула Ньютона-Лейбница (вывод). Если функция y=f(x) непрерывна на отрезке и F(x) - какая-либо её первообразная на (F"(x)=f(x)), то имеет место формула ∫(от a до b) f(x)dx=F(b)-F(a). Эта формула является формулой Ньютона-Лейбница.Рассмотрим тождество: F(b)-F(a)=F(x n)-F(x 0)=(F(x n)-F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1)-F(x 0)). Преобразуем каждую разность в скобках по формуле Лагранжа: f(b)-f(a)=f’(c)*(b-a). Получим F(b)-F(a)=F’(c n)(x n -x n -1)+F’(c n -1)(x n -1 -x n -2)+F’(c 2)(x 2 -x 1)+F’(c 1)(x 1 -x 0)= ΣF’(Ci)ΔXi=Σf(Ci)ΔXi, то есть F(b)-F(a)= Σf(Ci)ΔXi, где Ci есть некоторая точка интервала (X i -1 ,X i). Так как функция y=f(x) непрерывна на , то она интегрируема на . Поэтому существует предел интегральной суммы, равной определенному интегралу от f(x) на . Переходя к пределу при λ=maxΔXi→0,получаем F(b)-F(a)=lim Σf(Ci)ΔXi, то есть ∫(от a до b) f(x)dx=F(b)-F(a).

Функция z=f(x;y) называется дифференцируемой

11. Свойство дифференцируемой функции: связь между дифференцируемостью функции z=f(x;y) и непрерывностью функции z=f(x;y) в точке (формулировка, доказательство). Если функция z=f(x;y) дифференцируема в точке М(x;y), то она непрерывна в этой точке, имеет в ней частные производные. Доказательство . Пусть функция у=f(x) дифференцируема в точке х 0 . Дадим в этой точке аргументу приращение Δх. Функция получит приращение Δу. Найдем limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Следовательно, у=f(x) непрерывна в точке х 0 .

Билет №7

Необходимый признак экстремума.

Если непрерывная функция z=z(x,y) имеет в точке P0(x0,y0) экстремум, то все ее частные производные первого порядка в этой точке или равны нулю или не существуют

Докозательство: Частная производная функции z=f(x,y) по x в точке P0(x0,y0) есть производная функции одной переменной φ(x)=f(x,y0) в точке x-x0. Но в этой точке функция φ(x) имеет, очевидно, экстремум. Следовательно, φ’(x0)=0 .Так как φ’(x0)=f’x(x0,y0), то f’x(x0,y0)=0 Аналогично можно показать, что f’y(x0,y0)=0 . Теорема доказана.

Билет №8

6. Теорема о среднем (формулировка, доказательство, геометрический смысл). Если функция f(x) непрерывна на отрезке , то существует точка С∈ такая, что ∫(от a до b) f(x)dx=f(c)*(b-a).Доказательство . По формуле Ньютона-Лейбница имеем ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), где F"(x)=f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F"(c)*(b-a)=f(c)*(b-a).Геометрический смысл . Теорема при f(x)≥0 имеем простой геометрический смысл: значение определенного интеграла равно, при некотором С∈ (a;b), площади прямоугольника с высотой f(c) и основанием b-a. Число f(c)=1/(b-a)∫(от a до b) f(x)dx называется средним значением функции f(x) на отрезке .

8. Частные приращения функции z=f(x;y). Частные производные: определение и их геометрический смысл. Пусть задана функция z=f(х;у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной х приращение ∆х, сохраняя значение переменной у неизменным. Тогда функция z получит приращение, которое назовем частным приращением z по х и обозначим ∆ x z. Итак, ∆ x z=f(x+∆x;y)–f(х;у). Аналогично получаем частное приращение z по у: ∆ y z=f(x;у+∆y)–f(х;у).Если существует предел lim∆x→0(∆ x z/∆x)=lim∆x→0((f(x+∆x;y)-f(x;y))/∆x), то он называется частной производной функции z=f(x;y) в точке М(х;у) по переменной х и обозначается одним из символов: z" x , δz/δx; f" x , δf/δx. Геометрический смысл . Графиком функции z=f(x;y) является некоторая поверхность. График функции z=f(x 0 ;y 0) есть линия пересечения этой поверхности с плоскостью у=у 0 . Исходя из геометрического смысла производной для функции одной переменной, заключаем, что f" x (x 0 ;y 0)=tgα, где α - угол между осью Ох и касательной, проведённой к кривой z=f(x 0 ;y 0) в точке M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Аналогично f" y (x 0 ;y 0)=tgβ.

Билет №9

Доказательство Геометрический смысл

Касательной плоскостью Нормалью к поверхности

Билет №10

10. Определение дифференцируемой функции z=f(x;y) в точке. Определение полного дифференциала dz и его форма. Функция z=f(x;y) называется дифференцируемой в точке М(х;у), если её полное приращение в этой точке можно представить в виде: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, где α=α(∆x;∆y)→0 и β=β(∆x;∆y)→0 при ∆x→0 и ∆y→0. Главная часть приращения функции z=f(x;y), линейная относительно ∆x и ∆y, называется полным дифференциалом этой функции и обозначается символом dz: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.

Билет №11

4. Определение определённого интеграла по отрезку. Основные свойства определённого интеграла по отрезку (с доказательством одно из них). Определённым интегралом по отрезку от функции f(x) называется предел интегральной суммы Σf(c i)Δx i , если этот предел существует и не зависит ни от деления отрезка на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i .Свойства : 1)Если с - постоянное число и функция f(x) интегрируема на , то ∫(от a до b) с*f(x)dx=с*∫(от a до b) f(x)dx.2)Если функции f 1 (x) b f 2 (x) интегрируемы на , тогда интегрируема на их сумма и ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫(от a до b) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Если функция f(x) интегрируема на и a

10. Определение дифференцируемой функции z=f(x;y) в точке. Функция z=f(x;y) называется дифференцируемой в точке М(х;у), если её полное приращение в этой точке можно представить в виде: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, где α=α(∆x;∆y)→0 и β=β(∆x;∆y)→0 при ∆x→0 и ∆y→0.

12. Свойство дифференцируемой функции: связь между дифференцируемостью функции z=f(x,y) существованием частных производных в точке (формулировка, доказательство). Теорема: Если функция дифференцируема в точке, то в этой точке существуют конечные частные производные, числено равны А и В Дано: Δz=AΔx+ВΔy+0(ρ) Доказать: Ǝ(δz/δx(x 0 ;y 0)=A Доказательство: Дадим x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A+0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Аналогично: Y 0 →Δy, x=x 0 =>Δ y Z. δz/Δy(x 0 ;y 0)=B.

Билет №12

Доказательство

Билет №13

2. Задача о площади криволинейной трапеции, приводящая к понятию определённого интеграла по отрезку. Определение определённого интеграла по отрезку. Пусть на отрезке задана функция y=f(x)≥0. Фигура, ограниченная сверху графиком функции y=f(x), снизу - осью Ох, сбоку прямые x=a и x=b, называется криволинейной трапецией. Найдём площадь этой трапеции. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. C уменьшением всех величин Δx i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимаемся предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ=maxΔx i →0: S=lim n→∞ Sn=lim n→∞(λ→0) Σf(c i)Δx i , то есть S=∫(от a до b) f(x)dx. Итак, определённый интеграл от неопределённой функции численно равен площади криволинейной трапеции.Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка на численные отрезки, ни от выбора точек в них, то число I называется определённым интегралом от функции y=f(x) на отрезке и обозначается ∫(от a до b) f(x)dx. Таким образом, ∫(от a до b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. Касательная плоскость и нормаль к поверхности (определение). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 . Нормалью к поверхности в точке М называется прямая, проходящая через эту точку перпендикулярно касательной плоскости.

Билет №14

5. Теорема об оценке определённого интеграла по отрезку (формулировка, доказательство, геометрический смысл). Оценка интеграла. Если m и M - соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке , (aДоказательство . Так как для любого x∈ имеем m≤f(x)≤M, то ∫(от a до b) mdx≤ ∫(от a до b) f(x)dx≤∫(от a до b) Mdx. Получаем: m(b-a)≤∫(от a до b) f(x)dx≤M(b-a). Геометрический смысл . Площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть , а высоты равны m и M.

Билет №15

Билет №16

21. Производная функции u=u(x;y;z) по направлению l (определение). Предел LimΔl→0(Δu/Δl) называется производной функции u(x;y;z) по направлению вектора l в точке с координатами (x;y;z).

22. Градиент функции u=u(x;y;z) в точке (определение). Вектор с координатами (δu/δx; δu/δy; δu/δz) называется

Билет №17

7. Интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом (формулировка, доказательство). Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, то есть (∫(от a до x) f(t)dt)" x =f(x). Доказательство . По формуле Ньютона-Лейбница имеем: ∫(от a до x) f(t)dt=F(t)|(от a до x)=F(x)-F(a). Следовательно, (∫(от a до x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Это означает, что определённый интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

полное приращение непрерывной непрерывна

Билет №18

1. Первообразная функция. Теорема о разности двух первообразных (с доказательством). Неопределенный интеграл: определение, простейшие свойства неопределённого интеграла (с доказательством одно из них). Функция F(x) называется первообразной функцией f(x) на интервале (a;b), если для любого x∈(a;b) выполняется равенство F"(x)=f(x).Теорема . Если функция F(х) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задаётся формулой F(x)+C, где С=const.Доказательство . Функция F(x)+C является первообразной f(x). Действительно, (F(x)+C)"=F"(x)=f(x). Пусть Ф(х) - некоторая другая, отличная от F(x), первообразная функция f(x), т.е. Ф"(х)=f(x). Тогда для любого x∈(a;b) имеем (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x)-f(x)=0. А это означает, что Ф(х)-F(x)=C, C=const. Следовательно, Ф(x)=F(x)+C.Множество всех первообразных функций F(x)+C для f(x) называется неопределённым интегралом от функции f(x) и обозначается символом ∫f(x)dx.Свойства : 1) Дифференциал от неопределённого интеграла равен подынтегральному выражению, а производная неопределённого интеграла равна подынтегральной функции d(∫f(x)dx)=f(x)dx, (∫f(x)dx)"=f(x).d(∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. и (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) Постоянный множитель можно выносить за знак интеграла: ∫af(x)dx=a∫f(x)dx.4) Неопределённый интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx.5) (Инвариантность формулы интегрирования). Если ∫f(x)dx=F(x)+C, то и ∫f(u)du=F(u)+C, где u=φ(x) - произвольная функция, имеющая непрерывную производную.

22. Градиент функции u=u(x;y;z) в точке (определение, свойства). Связь между производной по направлению и градиентом функции (обоснование). Вектор с координатами (δu/δx; δu/δy; δu/δz) называется градиентом функции u=f(x;y;z) и обозначается gradU=(δu/δx; δu/δy; δu/δz). gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Свойства : 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, где u*v - скалярные произведения векторов u и v. Связь . Пусть задана функция u=u(x;y;z) и поле градиентов gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Тогда производная Δu/Δl по направлению некоторого вектора l равняется проекции вектора GradU на вектор l.

Билет №19

4. Определение определённого интеграла по отрезку. Основные свойства определённого интеграла по отрезку (с доказательством одно из них). Определённым интегралом по отрезку от функции f(x) называется предел интегральной суммы Σf(c i)Δx i , если этот предел существует и не зависит ни от деления отрезка на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i .Свойства : 1)Если с - постоянное число и функция f(x) интегрируема на , то ∫(от a до b) с*f(x)dx=с*∫(от a до b) f(x)dx. Доказательство. Составим интегральную сумму для функции с*f(x). Имеем Σс*f(c i)Δx i =с*Σf(c i)Δx i . Тогда lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(от a до b) f(x)dx. Отсюда вытекает, что функция с*f(x) интегрируема на и справедлива формула ∫(от a до b) с*f(x)dx= с*∫(от a до b) f(x)dx.2)Если функции f 1 (x) b f 2 (x) интегрируемы на , тогда интегрируема на их сумма и ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫(от a до b) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Если функция f(x) интегрируема на и a

17. Касательная плоскость и нормаль к поверхности (определение). Теорема о существовании касательной плоскости (формулровка, доказательство). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 .Нормалью к поверхности в точке М называется прямая, проходящая через эту точку перпендикулярно касательной плоскости.Теорема . Если δF/δx; δF/δy; δF/δz определены в окрестности точки Мо и непрерывны в самой точке М 0 и одновременно в нуль не обращаются, то все касательные прямые к линиям на поверхности лежат в одной плоскости. Доказательство . L: система(x=x(t); y=y(t); z=z(t)). Касательная прямая (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (поверхность). F(x(t), y(t), z(t))=0 сложная функция переменной t. пользуемся правилом дифференцируемости сложной функции: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt)+(δF/δz)*(dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+(δF(M 0)/δz)*z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); обозначим n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0)/δz); n⊥g. Поскольку через данную точку можно провести бесконечное множество линий, лежащих на поверхности, а к ним бесконечное множество касательных прямых, следовательно все касательные прямые лежат в одной плоскости.

Билет №20

9. Полное приращение функции z=f(x;y). Непрерывность функции z=f(x;y) в точке (два определения). Пусть задана функция z=f(x;y). Дадим независимой переменной х приращение ∆х, а переменной у приращение ∆у. Тогда полное приращение ∆z функции определяется равенством: ∆z=f(x+∆x;y+∆y)-f(x;y). 1)Функция z=f(х;у) называется непрерывной в точке М 0 (х 0 ;у 0)∈ D(z), если её предел в этой точке совпадает со значением функции в данной точке, т.е. limX→X 0 \Y→Y 0 (f(x;y))= f(x 0 ;y 0). 2)Функция z=f(х;у) непрерывна на множестве, если она непрерывна в каждой точке этого множества

Билет №21

21. Производная функции u=u(x;y;z) по направлению l (определение, формула для вычисления, вывод формулы вычисления). Предел LimΔl→0(Δu/Δl) называется производной функции u(x;y;z) по направлению вектора l в точке с координатами (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.Предположим, что функция u(x;y;z) непрерывна и имеет непрерывные производные по своим аргументам в области D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, где E 1 , E 2 , E 3 стремятся к нулю при Δl→0. Разделим всё равенство на Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Равенство можно представить так: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Перейдя к пределу, получим Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Билет №22

20. Достаточный признак существования экстремума функции z=f(x;y). (формулировка). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ>0, то функция f(x;y) в точке (X 0 ;Y 0) имеет экстремум: максимум, если A<0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №23

17. Касательная плоскость к поверхности (определение). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 .

18. Уравнения касательной плоскости к поверхности, заданной явно Явно. z=f(x;y) в точке Mo(Xo;Yo;Zo). K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Билет №24

Теорема 12. {Первый достаточный признак экстремума) Пусть х 0 - критическая точка непрерывной функции f(х). Если f" (х) при переходе через точку x 0 меняет знак с «+» на «-», то x 0 - точка локального максимума. Если f "(х) при переходе через точку х 0 меняет знак с «-» на «+», то х 0 - точка локального минимума. Если f "(х) при переходе через точку x 0 не меняет знак, то х 0 не является точкой локального экстремума.

Доказательство. Пусть x 0 - точка возможного экстремума функции, причем

f "(x)>0 для xx Э U (x 0 ,Дельта);

f "(x) х 0 , A x Э U (x 0 ,Дельта). Тогда

при f "(x)>0 для xx Э U (x 0 ,Дельта); => f(x 0 )>f(x),

При f "(x) х 0 , A x Э U (x 0 ,Дельта). => f(x 0 )
следовательно A x Э U (x 0 ,Дельта): f (x 0 )> f (x ), т. е. точка х 0 является точка локального максимума.

Аналогично доказывается и существование точки локального минимума. Если f `(x ) сохраняет знак в окрестности точки х 0 , то в этой окрестности функция монотонна, т. е. точка х 0 не является точкой локального экстремума.

Аннотация
Данная работа преследует несколько целей. Первая из которых заключается в изложении нового подхода к Платоновым телам (ПТ) Второй, не менее важной, целью являет освещение роли Платоновых тел в контексте развития математики и науки в целом.

Платоновы тела также рассматриваются и с более общих позиций – их симметрия, связь с «золотым сечением», их влияния на развитие математики и всего теоретического естествознания. Обсуждаются результаты их использования в науке прошлых веков («Божественная пропорция» Пачоли, «Космический кубок» Кеплера, «икосаэдрическая идея» Клейна). Приводятся примеры современных научных открытий, основанных на ПТ (квазикристаллы, фуллерены, новый подход к созданию теории элементарных частиц).

Уделяется внимание и роли Платоновых тел в создании «Начал» Евклида. Согласно «гипотезе Прокла» развитие математики, начиная с Евклида, осуществлялось в двух направлениях: «Классическая математика» (позаимствовала в «Началах» аксиоматический подход, теорию чисел и теорию иррациональностей) и «Математика гармонии» (основана на ПТ и «золотом сечении»).

На основании проделанной работы делается вывод: по своему влиянию на развитие математики и науки в целом Платоновы тела вместе с «золотым сечением» можно поставить в один ряд не только с теоремой Пифагора (Кеплер), но и с натуральными и иррациональными числами.
Содержание:

Платоновы тела
Симметрия Платоновых тел
Связь Платоновых тел с «золотым сечением»
Гипотеза Прокла: с какой целью Евклид написал свои «Начала»?
Новый взгляд на развитие математики, вытекающий из гипотезы Прокла
«Космический кубок» Иоганна Кеплера
Платоновы тела и «золотое сечение» в «Божественной пропорции» Луки Пачоли
Икосаэдрическая идея Феликса Клейна
Квазикристаллы Дана Шехтмана
Фуллерены (Нобелевская Премия по химии - 1996)
Новые подходы в теории элементарных частиц
Экспериментальное доказательство проявления «золотого сечения» в квантовом мире
Сюрпризы для теоретического естествознания
Заключение: Платоновы тела как уникальные геометрические объекты науки и природы
Литература

Пока алгебра и геометрия двигались каждая своим путем,

их прогресс был медленным, а приложения ограниченными.

Но когда эти науки объединили свои усилия, они

позаимствовали друг у друга новые жизненные силы

и с тех пор быстрыми шагами направились к совершенству

(Жозеф Луи Лагранж)

1. Платоновы тела

Правильные многогранники известны с древнейших времён. Но почему правильные многогранники называют Платоновыми телами?

Платон (428-348 до н.э.) в своих трудах много внимания уделил взглядам пифагорейцев на правильные тела, поскольку и сам считал, что вся Вселенная имеет форму додекаэдра, а материя состоит из атомов четырех типов, которые имеют форму тетраэдров, кубов, октаэдров и икосаэдров. Он первым воспел красоту правильных выпуклых многогранников, обладающих удивительной симметрией в трёхмерном пространстве. Грани этих многогранников – это правильные многоугольники с одинаковым числом сторон; в каждой вершине многогранников сходится одинаковое число рёбер. Примечательно, что все пять Платоновых тел в разные времена использовались в качестве игральных костей.

^ Теэтет Афинский (417 - 369 до н. э. ), современник Платона, дал математическое описание правильных многогранников и первое известное доказательство того, что их ровно пять.

После них эстафету принял Евклид (365-300 до н.э.). В заключительной книге знаменитых «Начал» Евклид дал не только полный, подробный анализ Платоновых тел, но и простейшее геометрическое доказательство существования не более пяти правильных тел.

Теории многогранников посвящено много книг. Одной из наиболее известных является книга английского математика М. Венниджера «Модели многогранников». В русском переводе эта книга опубликована издательством «Мир» в 1974 г. Эпиграфом к книге выбрано высказывание Бертрана Рассела: « Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».

Эта мысль Бертрана Рассела, прежде всего, может быть отнесена к правильным многогранникам, с которых и начинается книга М. Венниджера. Эти многогранники принято называть Платоновыми телами, названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии. Начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники.

Первый из них – это тетраэдр (Рис.1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.

(а)

(б)

(г) (д)

Рисунок 1. Платоновы тела: (а) тетраэдр («Огонь»), (б) гексаэдр или куб («Земля»), (в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр («Вселенский разум»)

Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (Рис.1-б). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями – октаэдр.

Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями – икосаэдр (Рис.1-г). Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (Рис. 1-в).

Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника –

пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (Рис.1-д).

Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим плоскость, то есть, из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. Из этих рассуждений вытекает, что существует только пять правильных многогранников, гранями которых могут быть только равносторонние треугольники, квадраты и пентагоны.

2. Симметрия Платоновых тел

С давних времен Платоновы тела привлекали внимание исследователей своими исключительными симметрическими свойствами. Обычно для характеристики симметрии некоторого объекта приводится полная совокупность элементов симметрии. Например, группа симметрий снежинки имеет вид L 6 6Р. Это означает, что снежинка имеет одну ось симметрии шестого порядка L 6 , то есть, может 6 раз «самосовмещаться» при повороте вокруг оси, и 6 плоскостей симметрии. Группа симметрий цветка ромашки, имеющего 24 лепестка, имеет вид L 24 24Р, то есть, цветок имеет одну ось 24-го порядка и 24 плоскости симметрии. В таблице 1 приведены группы симметрий всех «Платоновых Тел».

Таблица 1. Группы симметрий Платоновых тел

Многогранник	Форма граней	Симметрия
Тетраэдр	Равносторонние треугольники	4L 3 3L 2 6Р
Куб	Квадраты	3L 4 4L 3 6L 2 9Р С
Октаэдр	Равносторонние треугольники	3L 4 4L 3 6L 2 9Р С
Додекаэдр	Равносторонние пятиугольники	6L 5 10L 3 15L 2 15Р С
Икосаэдр	Равносторонние треугольники	6L 5 10L 3 15L 2 15Р С

Анализ симметрий «Платоновых Тел», приведенных в Табл. 1, показывает, что группы симметрий куба и октаэдра, а также додекаэдра и икосаэдра совпадают. Это связано с тем, что додекаэдр дуален икосаэдру, а куб дуален октаэдру. Анализ этой таблицы показывает, что додекаэдр и икосаэдр выделяются своими симметрическими свойствами среди других Платоновых тел. Группа симметрий 6L 5 10L 3 15L 2 15Р С означает, что додекаэдр и икосаэдр обладают 6 линиями симметрии 5-го порядка L 5 , 10 линиями симметрии 3-го порядка L 3 , 15 линиями симметрии 2-го порядка L 2 , 15 плоскостями симметрии Р и центром симметрии С.

^ 3. Связь Платоновых тел с « золотым сечением».

Анализ Платоновых тел на Рис. 1 показывает, что два Платоновых тела - додекаэдр и двойственный ему икосаэдр непосредственно связаны с «золотым сечением». Действительно, гранями додекаэдра (Рис. 1-д) являются пентагоны, т.е., правильные пятиугольники, основанные на золотом сечении. Если внимательно посмотреть на икосаэдр (Рис. 1-г), то можно увидеть, что в каждой вершине икосаэдра сходится пять треугольников, внешние стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что «золотое сечение» играет существенную роль в конструкции этих двух Платоновых тел.

Но существуют более глубокие математические подтверждения фундаментальной роли, которую играет золотое сечение в икосаэдре и додекаэдре. Известно, что эти тела имеют три специфические сферы. Первая (внутренняя) сфера вписана в тело и касается его граней. Обозначим радиус этой внутренней сферы через R i . Вторая или средняя сфера касается ее ребер. Обозначим радиус этой сферы через R m . Наконец, третья (внешняя) сфера описана вокруг тела и проходит через его вершины. Обозначим ее радиус через R c . В геометрии доказано, что значения радиусов указанных сфер для додекаэдра и икосаэдра,

имеющего ребро единичной длины, выражается через золотую пропорцию:
(Табл.2).

Таблица 2. Золотая пропорция в сферах додекаэдра и икосаэдра

Заметим, что отношение радиусов одинаково, как для икосаэдра, так и

для додекаэдра. Таким образом, если додекаэдр и икосаэдр имеют одинаковые вписанные сферы, то их описанные сферы также равны между собой. Доказательство этого математического результата дано в Началах Евклида.

В геометрии известны и другие соотношения для додекаэдра и икосаэдра, подтверждающие их связь с золотой пропорцией. Таким образом, существует огромное количество соотношений, полученных еще античными математиками, подтверждающих замечательный факт, что именно золотое сечение является главной пропорцией додекаэдра и икосаэдра, и этот факт является особенно интересным с точки зрения так называемой « додекаэдро- икосаэдрической доктрины» .

Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них.

Первое достаточное условие экстремума.

Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда

Другими словами:

Алгоритм.

Находим область определения функции.

Находим производную функции на области определения.

Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называют точками возможного экстремума , проходя через эти точки, производная как раз может изменять свой знак).

Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.

Пример. Найти экстремумы функции .
Решение.
Областью определения функции является все множество действительных чисел, кроме x = 2 .
Находим производную:

Нулями числителя являются точки x = -1 и x = 5 , знаменатель обращается в ноль при x = 2 . Отмечаем эти точки на числовой оси

Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x = -2, x = 0, x = 3 и x = 6 .

Следовательно, на интервале производная положительна (на рисунке ставим знак плюс над этим интервалом). Аналогично

Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.

Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.
В точке x = -1 функция непрерывна и производная меняет знак с плюса на минус, следовательно, по первому признаку экстремума, x = -1 – точка максимума, ей соответствуем максимум функции .
В точке x = 5 функция непрерывна и производная меняет знак с минуса на плюс, следовательно, x = -1 – точка минимума, ей соответствуем минимум функции .
Графическая иллюстрация.

Ответ: .

Второй достаточный признак экстремума функции.
Пусть ,

если , то - точка минимума;

если , то - точка максимума.

Как видите, этот признак требует существования производной как минимум до второго порядка в точке .
Пример. Найти экстремумы функции .
Решение.
Начнем с области определения:

Продифференцируем исходную функцию:

Производная обращается в ноль при x = 1 , то есть, это точка возможного экстремума.
Находим вторую производную функции и вычисляем ее значение при x = 1 :

Следовательно, по второму достаточному условию экстремума, x = 1 - точка максимума. Тогда - максимум функции.
Графическая иллюстрация.

Ответ: .
Третий достаточный признак экстремума функции.
Пусть функция y = f(x) имеет производные до n -ого порядка в -окрестности точки и производные до n+1 -ого порядка в самой точке . Пусть и .
Тогда,

Конец работы -

Эта тема принадлежит разделу:

Алгебра и аналитическая геометрия. Понятие матрица, операции над матрицами и их свойства

Понятие матрица операции над матрицами и их свойства.. матрица это прямоугольная таблица составленная из чисел которые нельзя.. а сложение матриц поэлементная операция..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Определение дифференцируемости
Операция нахождения производной называется дифференцированием функции. Функция называется дифференцируемой в некоторой точке, если она имеет в этой точке конечную производную, и

Правило дифференцирования
Следствие 1. Постоянный множитель можно выносить за знак производной:

Геометрический смысл производной. Уравнение касательной
Углом наклона прямой y = kx+b называют угол, отсчитываемый от полож

Геометрический смысл производной функции в точке
Рассмотрим секущую АВ графика функции y = f(x) такую, что точки А и В имеют соответственно координаты

Решение
Функция определена для всех действительных чисел. Так как (-1; -3) – точка касания, то

Необходимые условия экстремума и достаточные условия экстремума
Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых

Условия монотонности и постоянства функции
Условие (нестрогой) монотонности функции на интервале. Пусть функция имеет производную в каж

Определение первообразной
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство

Проверка
Для проверки результата продифференцируем полученное выражение: В итоге получи

Первообразная произведения константы и функции равна произведению константы и первообразной функции
Достаточным условием существования первообразной у заданной на отрезке функции являе

Определение
Пусть определена на

Геометрический смысл
Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми

Свойства определенного интеграла
Основные свойства определенного интеграла. Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирован

Формула Ньютона-Лейбница (с доказательством)
Формула Ньютона-Лейбница. Пусть функция y = f(x) непрерывна на отрезке и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо рав

Функция y = f(x) называется возрастающей (убывающей ) в некотором интервале, если при x 1 < x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) > f(x 2)).

Если дифференцируемая функция y = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f " (x) > 0

(f " (x) < 0).

Точка x о называется точкой локального максимума (минимума ) функции f(x), если существует окрестность точки x о , для всех точек которой верно неравенство f(x) ≤ f(x о) (f(x) ≥ f(x о)).

Точки максимума и минимума называются точками экстремума , а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума . Если точка x о является точкой экстремума функции f(x), то либо f " (x о) = 0, либо f (x о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x о - критическая точка. Если f " (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную
f " (x) в окрестности точки x о и вторую производную в самой точке x о . Если f " (x о) = 0, >0 ( <0), то точка x о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Исследование условий и построение графиков.

Найти область определения функции

Найти точки пересечения графика с осями координат

Найти интервалы знака постоянства

Исследовать на четность, нечетность

Найти асимптоты графика функции

Найти интервалы монотонности функции

Найти экстремумы функции

Найти интервалы выпуклости и точки перегиба

Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры.

Вертикальная

Вертикальная асимптота - прямая вида при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

[править]Горизонтальная

Горизонтальная асимптота - прямая вида при условии существования предела

[править]Наклонная

Наклонная асимптота - прямая вида при условии существования пределов

Пример наклонной асимптоты

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при , и из выше указанных замечаний следует, что

1. Функция имеет или только одну наклонную асимптоту, или одну вертикальную асимптоту, или одну наклонную и одну вертикальную, или две наклонных, или две вертикальных, либо же вовсе не имеет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.